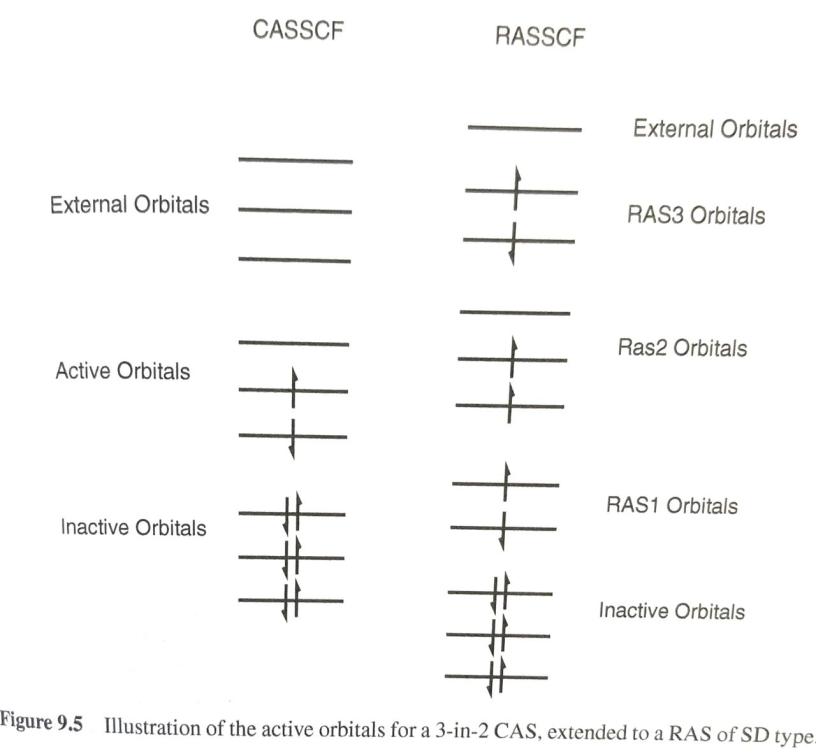
There are basically two kinds of electron correlation: static and dynamic. The former is mostly related to the lack of ab initio methods, namely Hartree-Fock, to fully describe the state of a polyelectronic system with a single electron configuration (described in turn by a single Slater determinant), therefore the use of Multiconfigurational methods ensures a better treatment of the static electron correlation by using wave functions constructed as linear combination of various Slater determinants. However, the more configurations included the harder it is to handle the problem from a computational standpoint and some approximations have to be made. One of such approximations consists in restricting the so-called active space allowing for only single and double excitations from the most important orbitals (in terms of occupation) or by restricting the number of electrons to be promoted in various excited state configurations.
As part of our research on Multi-Excimeric states for describing exciton transference between photosynthetic pigments, we have had to make use of the RAS-2SF approximation as implemented in Q-Chem 5.0 by Prof. David Casanova from the Donostia International Physics Center.
The following is a thorough tutorial on the use of Q-Chem 5.x for RAS-2SF calculations mostly written by Gustavo “Gus” Mondragón, who extensively used this method during his photosynthesis research.
The first step, before the RAS-nSF calculations is a geometry optimization, even if you work with x-ray structures, a constrained hydrogen optimization could increase accuracy. Then, we need to calculate a single-point energy using RAS. Comments in the input file can be inserted by placing a “!” sign before the comment:
$rem
jobtype sp !We set the calculation as a single point one
exchange HF !The calculation is performed by ab initio Hartree-Fock method
basis BASIS SET !Set the basis of your choice and needs
unrestricted false !Set if your calculation is spin restricted or unrestricted.
max_scf_cycle CYCLES !SCF cycles. Default 150
mem_total MEMORY !Total memory for your calculation.
gui 2 !Calls a CHK file
molden_format true !Print the information into a MOLDEN format, you can open the MO graphics
print_orbitals N !Set the number of virtual orbitals to print
$end
$molecule
0 1
...
$endThis performs a single point Hartree-Fock calculation for the exchange energy at the ground state assuming a singlet spin multiplicity. The “molden_format” line allows you to print the information of your Q-Chem work into a MOLDEN format, and use it to visualize the molecular orbitals of your calculation, and in the “print_orbitals” line we need to specify not only if we want to print the orbitals, but also how many virtual orbitals we want to print (by default, all occupied ones are printed by specifying “true” keyword, plus 5 virtual orbitals), so if we want to print 25 additional virtual orbitals instead of the occupied ones, we replace “N” with “25”, which will be printed in the output. As with Gaussian, you can establish various calculations, but you must write after “$end” of molecular coordinates:
$molecule
...
$end
---blank line---
@@@
---blank line---
$rem
...
$endThe line @@@ is similar to the use of –Link1– in Gaussian.
the next step is a single-point calculation of the molecule at the spin multiplicity of interest. For example, for singlet fission, we use a quintet as the final multiplicity because it is similar to the state we’re looking for and will thus help us to build the required wavefunction for SF.
$molecule
...
$end
---blank line---
@@@
---blank line---
$rem
scf_guess read
jobtype sp
exchange HF
basis BASIS SET
gui 2
$end
---blank line---
$molecule
0 5
read
$endWe now need to establish the active space for the excited states calculation. It is convenient to fragment our molecule to work with RAS by using the “ras_nfrag” and “ras_nfrag_atoms” keywords, we only need to know the atomic coordinates well and I highly recommend to pay attention if the atoms of your molecules are ordered by coordinates, this shall facilitate your work when you get at this point. With the identification of fragments, also a molecular orbitals localization is recommended. As the molecular fragments are built, the molecular orbitals also must be localized in them. Avoiding this step increases the computational cost. This will localize the active space orbitals as well as the virtual and occupied ones. This part is controlled by using the “ras_frag_mo” and “ras_mo_sets” keywords. RAS-CI can be called with the “correlation” keyword. As usual, we need to specify the number of desired roots.
$molecule
...
$end
@@@
$rem
exchange HF
basis BASIS SET
unrestricted false
max_scf_cycles CYCLES
gui 2
mem_total MEMORY
correlation rasci !Here's the RAS-CI method. RAS-CI2 does not calculate excitonic states
ras_roots ROOTS !Set how many roots you want
ras_act ORB !Set the amount of orbitals in the active space (AS)
ras_elec ELEC !Set how many electrons are in the AS
ras_act_orb [a,b,c,...,u] !Specify the molecular orbital numbers, separated by a comma.
ras_occ OC !Specify how many orbitals (excluding the ones at AS) are occupied
max_cis_cycles CYCLES !Specify the cycles of the CI-AS
ras_spin_mult X !Set the spin multiplicity of interest
ras_nfrag F !Set how many fragments do you
ras_nfrag_atoms [xxx,yyy] !Set the atoms involved by fragment
ras_frag_mo MO !Set if you want to localize molecular orbitals. If you want to, MO=1
ras_frag_sets [XXX,H,P] !Set how many molecular orbitals are gonna be localized. XXX: MO's number.
n_frozen_core fc
ras_print 2
molden_format true
print_orbitals ORB
scf_guess read
$end
---blank line---
$molecule
0 MULT
read
$endImagine you want to calculate the singlet fission process in a pentacene dyad; each (optimized) molecule has 36 atoms. If I want to calculate RAS-2SF on this dyad by using aug-cc-pVDZ basis set, with an active space composed of 4 electrons and 4 molecular orbitals by calculating 10 roots, assuming the dyad’s HOMO-1 (145th molecular orbital) and LUMO (147th molecular orbital) are localized on one pentacene molecule and HOMO (146-th molecular orbital) and LUMO+1 (148-th molecular orbital) are localized into the another one, the RAS-2SF input would look like this:
$rem
exchange HF
basis aug-cc-pvdz
unrestricted false
max_scf_cycles 200
gui 2
mem_total 5000
correlation rasci
ras_roots 10
ras_act 4
ras_elec 4
ras_act_orb [145,146,147,148]
ras_occ 144
max_cis_cycles 400
ras_spin_mult 1
ras_nfrag 2
ras_nfrag_atoms [36,36]
ras_frag_mo 1
ras_frag_sets [144,2,2]
n_frozen_core fc
ras_print 2
molden_format true
print_orbitals 10
scf_guess read
$end
$molecule
0 5
read
$endHow to read the output?
Actually, not even the input building, but the output reading could be a real headache. The relevant part of the output is localized under the title R A S M A N 2, Because of the way the wave function is constructed there’s more than one excitation energy and the associate oscillator strength. Per excited state, it looks like this:
RAS-CI total energy for state 2: -5029.723674868694
Excitation energy (eV) = 1.5408
Multiplicity: Singlet
Dipole Moment: -2.5888 X 2.7531 Y 2.8019 Z
Trans. Moment: 0.0000 X -0.0000 Y -0.0000 Z
Strength : 0.000000
Amplitudes :
| HOLE | ALPHA | BETA | PART | AMPLITUDE
--------------------------------------------------
| | 1100 | 1100 | | 0.9199846
| | 1001 | 1001 | | -0.2026181
| | 0110 | 0110 | | -0.1970316
--------------------------------------------------
*** Contributions RASCI wfn Active: 93.59
Hole: 3.59
Part: 2.81
*** Unpaired Electrons
Yamaguchi: 0.74
*** Fragment decomposition for state: 1
--------------------------------------------------
*** Fragment weights
GS LE ME CR Total
0.8464 0.1460 0.0067 0.0009 1.0000
Local Excitons (LE)
A B Total
SE 0.0321 0.0287 0.0609
ME 0.0419 0.0433 0.0852
0.0740 0.0720 0.1460
Dimer Excitons (DE)
SS TT Total
0.0067 0.0000 0.0067
Charge Ressonances (CR)
A-->B B-->A Total
0.0004 0.0005 0.0009
Fragment # electrons
1 410.0001
2 409.9999Let’s analyze the output section by section. The first section looks like this:
RAS-CI total energy for state 2: -5029.723674868694
Excitation energy (eV) = 1.5408
Multiplicity: Singlet
Dipole Moment: -2.5888 X 2.7531 Y 2.8019 Z
Trans. Moment: 0.0000 X -0.0000 Y -0.0000 Z
Strength : 0.000000The first line corresponds to the total energy (in Hartrees) for the excited state, and the second line the energy difference between the ground state and the “nth” excited state. Also the transition dipole moment is shown. A crucial data for an excited state is the oscillator strength, given by the sord “Strength”. In this case, the oscillator strength is equal to 0.00000 (which means that the 2nd excited state is a dark state).
In the second section, we have the AS contributions and the unpaired electrons:
Amplitudes:
| HOLE | ALPHA | BETA | PART | AMPLITUDE
--------------------------------------------------
| | 1100 | 1100 | | 0.9199846
| | 1001 | 1001 | | -0.2026181
| | 0110 | 0110 | | -0.1970316
--------------------------------------------------
*** Contributions RASCI wfn Active: 93.59
Hole: 3.59
Part: 2.81
*** Unpaired Electrons
Yamaguchi: 0.74The “Amplitudes” part corresponds to the orbital transitions contributions to the AS part. In the table, the “ALPHA” and “BETA” sections are the alpha and beta electrons in the orbitals involved in the active space. We can look the first row:
The “HOLE” column correspond to the occupied orbitals, the “PART” column correspond to the virtual orbitals, and the numbers “1100” in the “ALPHA” and “BETA” sections correspond to the occupancy in the active space orbitals, the three sections give to us the whole description for a RAS calculation. We can read this like follows: the HOMO-1 and the HOMO orbitals are occupied, each orbital, by an alpha-spin electron, and also this orbitals are occupied, each one, by an beta-spin electron.
Also we can see the contribution to the RAS wave function, we need to remember that the RAS wave function is built by a layer of occupied orbitals, an AS layer and a virtual orbitals layer. In this specific case, we realize that a high contribution corresponds to the AS layer. Also we can look how many unpaired electrons are in our state, given by Yamaguchi’s approach.
The second section appears like this:
*** Fragment decomposition for state: 1
--------------------------------------------------
*** Fragment weights
GS LE ME CR Total
0.8464 0.1460 0.0067 0.0009 1.0000
Local Excitons (LE)
A B Total
SE 0.0321 0.0287 0.0609
ME 0.0419 0.0433 0.0852
0.0740 0.0720 0.1460
Dimer Excitons (DE)
SS TT Total
0.0067 0.0000 0.0067
Charge Ressonances (CR)
A-->B B-->A Total
0.0004 0.0005 0.0009The “Fragment weights” segment refers to a RAS wavefunction descomposition into a ground state (GS), Local Excitons (LE), Dimer Excitons (DE) and Charge Resonances (CR) wavefunctions. At the same time (excepting ground state), each wavefunction is decomposed into other ones:
- Local Excitons: This wavefunction is decomposed into single excitons (SE) and multiple excitons (ME) wavefunctions. On this specific example, we will read this part:
Local Excitons (LE)
A B Total
SE 0.0321 0.0287 0.0609
ME 0.0419 0.0433 0.0852
0.0740 0.0720 0.1460This implies that from a dyad A-B of pigments, there’s a 14.6% composition of Local Excitons wavefunction, and the excitons are more probable to be localized into A than into B, which means a low local exciton character.
- Dimer Excitons: This wavefunction describes two molecules A-B simultaneously excited with two coupled multiplicities: singlet-singlet (SS) and triplet-triplet (TT). So, our example would be read like follows:
Dimer Excitons (DE)
SS TT Total
0.0067 0.0000 0.0067If our dyad could be doubly excited simultaneously, the dimeric exciton wavefunction indicates that the (SS) state is more probable than the (TT) one.
And the third wavefunction:
- Charge Resonances: It corresponds to an A<->B electron exchange. This wavefunction is decomposed into the two possibilities: A->B transfer and B->A transfer, resulting, on the first case, an A cation and a B anion and viceversa. So, from this output:
Charge Ressonances (CR)
A-->B B-->A Total
0.0004 0.0005 0.0009Which can be interpreted as that there’s a little probable that the charge transfer goes from B to A, than from A to B. Usually, for singlet fission a low charge resonance character is required, but it is necessary for the multiexciton character to predominate.
If we remember from the beginning, the RAS-nSF approach works by fragmenting the system into two subsystems. It also gives to us an electron recount by fragment, per excited state:
Fragment # electrons
1 410.0001
2 409.9999The sum of both gives the total electrons. These electrons are usually constant into all states, excepting all states where CR wavefunction is high. The conclusion for this specific excited state is that: because of the high ground state character, it wouldn’t be allowed and becomes into a dark state.
Also, singlet fission is an adiabatic exciton transfer mechanism. The adiabatic nexus between two excited states is not trivial to calculate, but the one-particle density transition matrix norm approach is used, this will give to us the nonadiabatic coupling between two states. This section looks like follows:
Norm of the One-Particle Transition Density Matrix
State | 1 2 3 4 5 6
1 | - 0.0000 0.0001 0.0000 0.2599 0.0000
2 | 0.0000 - 0.0648 0.6921 0.0000 0.1643
3 | 0.0001 0.0648 - 0.0797 0.0000 0.1530
4 | 0.0000 0.6921 0.0797 - 0.0000 0.1574
5 | 0.2599 0.0000 0.0000 0.0000 - 0.0000
6 | 0.0000 0.1643 0.1530 0.1574 0.0000 -Each element is the one-particle density transition matrix norm between the horizontal and the vertical state. If we want to try if singlet fission is possible between two molecules, first, we need to characterize the Multi Excitonic microstates 1(TT), 3(TT) and 5(TT), and the excimer state. By characterizing these, next step is find this matrix, and look if the one-particle density transition matrix norm between the two states, the excimeric one and the 1(TT) one (this because of selection rules), is significantly greater than zero. By getting all this requirements, we can say that singlet fission is possible in our dyad.
This rather long post is the result of a long exercise of calculating the singlet fission properties of naturally occurring molecules in our laboratory. Thanks to Dr. Gustavo Mondragón and to Dr. María Eugenia Sandoval for their help in implementing these methodologies into our lab. If you find this post useful, please like it and share it.
Dear professor
We are working on some Biradicaloid molecules, but we don’t have Qchem software and good computational facility. If you could collaborate with us to screen the feasibility of singlet fission based on energetic criteria for our molecules, using RAS-2SF method, so that we can have understand these system and your perceptions on research to improve ourselves .
regards
Anup Thomas
Assistant Professor
Dept. Of Applied Science
SCTCE